Design vonphotonischintegrierter Schaltkreis
Photonische integrierte Schaltungen(PIC) werden oft mithilfe mathematischer Skripte entworfen, da die Weglänge in Interferometern oder anderen Anwendungen, die empfindlich auf die Weglänge reagieren, eine wichtige Rolle spielt.BILDDie Herstellung erfolgt durch Strukturierung mehrerer Schichten (typischerweise 10 bis 30) auf einem Wafer. Diese Schichten bestehen aus vielen polygonalen Formen, die häufig im GDSII-Format dargestellt werden. Vor der Übermittlung der Datei an den Fotomaskenhersteller ist eine Simulation des photonischen integrierten Schaltkreises (PIC) zur Überprüfung der Designkorrektheit dringend zu empfehlen. Die Simulation ist in mehrere Ebenen unterteilt: Die unterste Ebene ist die dreidimensionale elektromagnetische (EM) Simulation. Hierbei wird die Simulation im Subwellenlängenbereich durchgeführt, obwohl die Wechselwirkungen zwischen den Atomen im Material auf makroskopischer Ebene behandelt werden. Typische Methoden sind die dreidimensionale Finite-Differenzen-Methode im Zeitbereich (3D-FDTD) und die Eigenmodenentwicklung (EME). Diese Methoden sind zwar am genauesten, aber für die gesamte Simulationszeit des PIC unpraktisch. Die nächste Ebene ist die 2,5-dimensionale EM-Simulation, beispielsweise die Finite-Differenzen-Strahlpropagation (FD-BPM). Diese Methoden sind deutlich schneller, weisen jedoch eine geringere Genauigkeit auf und können nur paraxiale Ausbreitung berücksichtigen. Sie eignen sich beispielsweise nicht zur Simulation von Resonatoren. Die nächste Stufe ist die 2D-EM-Simulation, beispielsweise mit 2D-FDTD und 2D-BPM. Diese Verfahren sind zwar schneller, bieten aber nur eingeschränkte Funktionalität; so können sie beispielsweise keine Polarisationsrotatoren simulieren. Eine weitere Stufe ist die Transmissions- und/oder Streumatrix-Simulation. Jede Hauptkomponente wird auf eine Komponente mit Ein- und Ausgang reduziert, und der angeschlossene Wellenleiter wird auf ein Phasenverschiebungs- und Dämpfungselement reduziert. Diese Simulationen sind extrem schnell. Das Ausgangssignal wird durch Multiplikation der Transmissionsmatrix mit dem Eingangssignal ermittelt. Die Streumatrix (deren Elemente als S-Parameter bezeichnet werden) multipliziert die Eingangs- und Ausgangssignale auf der einen Seite, um die Eingangs- und Ausgangssignale auf der anderen Seite der Komponente zu bestimmen. Im Wesentlichen enthält die Streumatrix die Reflexionen innerhalb des Elements. Die Streumatrix ist üblicherweise in jeder Dimension doppelt so groß wie die Transmissionsmatrix. Zusammenfassend lässt sich sagen, dass von der 3D-EM-Simulation bis zur Transmissions-/Streumatrix-Simulation jede Simulationsebene einen Kompromiss zwischen Geschwindigkeit und Genauigkeit darstellt. Entwickler wählen daher die für ihre spezifischen Anforderungen geeignete Simulationsebene, um den Validierungsprozess des Designs zu optimieren.
Die alleinige Verwendung elektromagnetischer Simulationen einzelner Elemente und einer Streu-/Transfermatrix zur Simulation des gesamten PIC garantiert jedoch kein vollständig korrektes Design vor der Strömungsplatte. Beispielsweise bleiben falsch berechnete Weglängen, Multimode-Wellenleiter, die Moden höherer Ordnung nicht effektiv unterdrücken, oder zwei zu nahe beieinander liegende Wellenleiter, die zu unerwarteten Kopplungsproblemen führen, während der Simulation wahrscheinlich unentdeckt. Obwohl fortschrittliche Simulationswerkzeuge leistungsstarke Validierungsmöglichkeiten bieten, erfordert dies daher weiterhin ein hohes Maß an Wachsamkeit und sorgfältiger Prüfung durch den Entwickler, kombiniert mit praktischer Erfahrung und technischem Wissen, um die Genauigkeit und Zuverlässigkeit des Designs zu gewährleisten und das Risiko im Strömungsschema zu minimieren.
Eine Technik namens Sparse FDTD ermöglicht die direkte Durchführung von 3D- und 2D-FDTD-Simulationen an einem kompletten PIC-Design zur Validierung des Entwurfs. Obwohl die Simulation eines sehr großen PIC für elektromagnetische Simulationswerkzeuge schwierig ist, kann Sparse FDTD einen relativ großen lokalen Bereich simulieren. Bei der traditionellen 3D-FDTD-Simulation werden zunächst die sechs Komponenten des elektromagnetischen Feldes innerhalb eines bestimmten quantisierten Volumens initialisiert. Im Zeitverlauf wird die neue Feldkomponente im Volumen berechnet usw. Jeder Schritt ist rechenintensiv und daher zeitaufwendig. Sparse 3D FDTD berechnet nicht in jedem Schritt an jedem Punkt des Volumens, sondern führt eine Liste von Feldkomponenten, die theoretisch einem beliebig großen Volumen entsprechen kann und nur für diese Komponenten berechnet wird. In jedem Zeitschritt werden Punkte, die an Feldkomponenten angrenzen, hinzugefügt, während Feldkomponenten unterhalb einer bestimmten Leistungsschwelle verworfen werden. Für manche Strukturen kann diese Berechnung um mehrere Größenordnungen schneller sein als die traditionelle 3D-FDTD-Simulation. Sparse FDTD-Verfahren eignen sich jedoch nicht für dispersive Strukturen, da sich das Zeitfeld zu stark ausbreitet, was zu zu langen und schwer handhabbaren Listen führt. Abbildung 1 zeigt einen Beispiel-Screenshot einer 3D-FDTD-Simulation, die einem Polarisationsstrahlteiler (PBS) ähnelt.
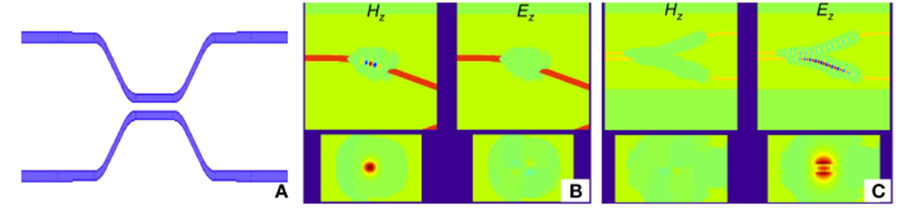
Abbildung 1: Simulationsergebnisse der 3D-Sparse-FDTD-Methode. (A) Draufsicht auf die simulierte Struktur, einen Richtkoppler. (B) Screenshot einer Simulation mit Quasi-TE-Anregung. Die beiden oberen Diagramme zeigen die Draufsicht auf die Quasi-TE- und Quasi-TM-Signale, die beiden unteren Diagramme die zugehörigen Querschnitte. (C) Screenshot einer Simulation mit Quasi-TM-Anregung.
Veröffentlichungsdatum: 23. Juli 2024





